What can I expect from this course?

This course is research-project-based. As a result, in order to excel at completing all course goals, you will have to spend at least 10 hours of focused work per week on homework and developing your research project outside class.
Course goals are: to understand, develop, and use deep generative models for audio (and other signals).
You will demonstrate that you have achieved the course goals by:
- Completing a series of homework exercises covering theory and software development for music information retrieval, processing of big datasets, and design and optimization of state-of-the-art deep neural networks
- Demonstrating knowledge of current research literature in the field by participating in class with insightful, critical, and creative perspectives about the latest developments in the field
- Conceiving a novel research question and carrying out a high-quality research project using the techniques used in the course
Optional (but recommended if you have excelled at completing all course goals): submit your work to be included in an upcoming peer-reviewed publication, such as

Example Generative models

Sounds are pressure waves moving over time and space.
The movement of pressure waves can be sensed by a membrane (i.e. such as the ones in a microphone) as they move through the membrane.
The membrane’s back-and-forth motions can be “digitized”.
Digitizing involves sampling and quatization.
A sampling rate comes with its Nyquist limit, which is half the sampling rate. Frequencies above the Nyquist limit will “alias” when digitized.
Digitization of a “time signal” requires the use of filtering to avoid aliasing of frequency content.
Exercise: draw the signal-flow diagram in an analog to digital converter. Include as much detail as possible.
After proper digitization, we end up with a “time-series” signal with an associated sampling rate, bit depth, and computer number format.
Is the dimensionality of digital audio small or big? What are benefits and pitfalls that result from this? Is digital audio data dense or sparse?

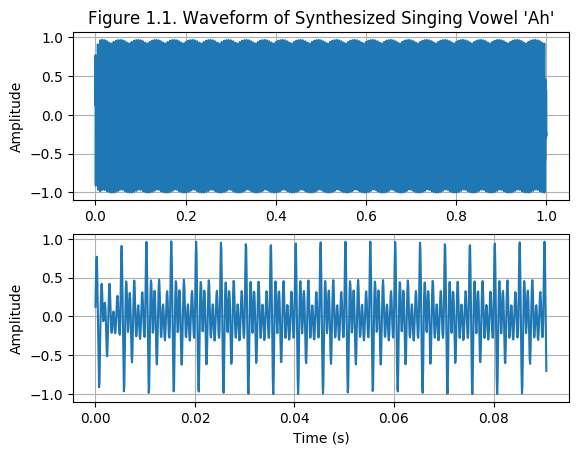
drawing

Very often, the most important content of digital time-domain signals relates to frequencies (i.e. pitch, envelopes, oscillations, etc.).
Fortunately, we can use the DFT to convert a discrete signal (or function) into a complex-valued function of frequency.
The DFT is a simple matrix-vector operation (dot product of the finite signal x(t) with each row of the complex-valued DFT matrix).
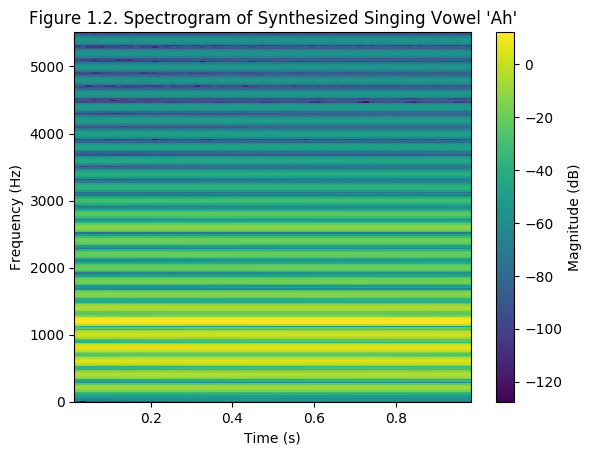
In the frequency domain, we can measure the magnitude (or energy, usually in decibels) in each of the frequency bins that we obtain after carrying out the DFT.

drawing

Figure 1.2 shows a spectrogram. What is the relationship between a spectrogram and the DFT? (and what about the FFT?)
Does the DFT create or solve issues associated with the dimensionality of digital audio?

More things to do:
- Find and read research papers that align with your interests in the proceedings of conferneces such as ISMIR 2021, CogMIR 2019, ICASSP 2021, DAFX 2021, or do a search on google scholar for keywords that better match your interests within the scope of this course.